第24题：

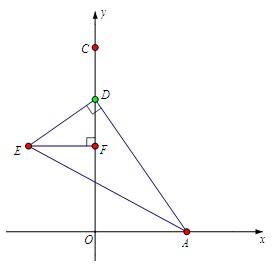
题目：在平面直角坐标系中，二次函数y=ax²+6x+c的图像经过点A(4，0)、B(-1，0)，与y轴交于点C，点D在线段OC上，OD=t，点E在第二象限，∠ADE=90°，tan∠DAE=1/2，EF⊥OD，垂足为F。

⑴求这个二次函数的解析式；

⑵求线段EF、OF的长(用含t的代数式表示)；

⑶当∠ECA=∠OAC时，求t的值.

【评论】

⑴根据函数解析式中，b=6，所以只需将A(4,0)、B(-1,0)代入解析式

求解，得：y=-2x²+6x+8

⑵充分利用tan∠DAE=1/2，

眼光放宽，得到DE/AD=1/2

再眼光放宽，DE、DA分别是RT△DEF和RT△ADO的斜边

再再眼光放宽，RT△DEF∽RT△ADO(万恶的余角)

再再再眼光放宽，EF/DO=DE/AD=FD/OA=1/2得到EF=1/2t，FO=t-2

⑶题目给的唯一条件是"∠ECA=∠OAC"

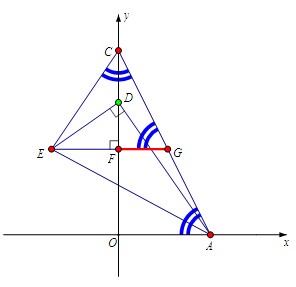
这个条件，给我的一个"微光"就是2011年的第25题

也是添平行线，做一个角度的转移

如右图，将∠OAC转移到了∠FGC

大家看到了什么呢？

是不是看到了"等腰△CEG"

那么后面就简单了啊！将两条线段表示出来，即可！

∵tan∠CGF=tan∠CAO=1/2，又CF=8-(t-2)=10-t

∴FG=5-1/2t

那么EG=EF+FG=1/2t+5-1/2t=5(太开心了啊~~)

由于E(-1/2t，t-2)C(0,8)而EC=5

所以化简，得t²-16t+60=0解得：t₁=6或者t₂=10

由于点D在线段OC上所以t₂=10，舍去即，t=6

P.S我还是喜欢我这种方法，我是个头脑简单的人

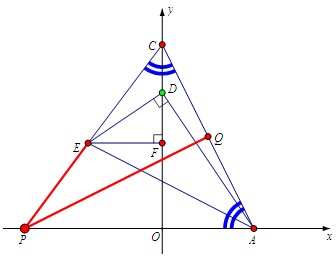
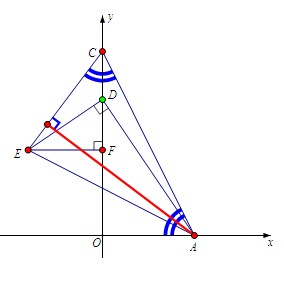
当然有多种方法：

放大的等腰三角形：

两点之间距离+勾股定理：

点击下一页查看25题详细点评